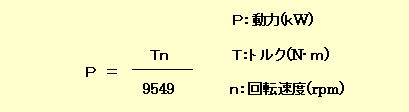
|
5.2 トルク・回転数・動力
図に示すように、半径R(m)の円板がその接線方向にF(N)の力を受けてn(rpm)で回転している場合を考える。円板を回転させようとする作用の大きさをトルクと言い、接線力と回転半径の積で表される。
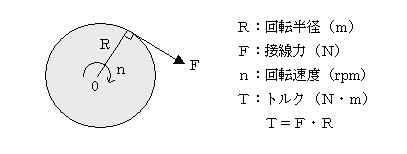
すなわち、
トルクT(N・m)=接線力F(N)×回転半径R(m) ………(1)
ここで、1分間に行う仕事を考えると、
仕事L(N・m)=力F(N)×移動距離S(m)
=F(N)×2πRn(m)
=2πRFn(N・m)
=2πTn(N・m)

〔備考〕
重力単位系で表わすと、上式は、トルクT(kgf・m)、回転速度n(rpm)として、
動力(仕事率)P= Tn/975 (kW)
|
|
| 〔演習問題〕 |
|
【問題5.2】
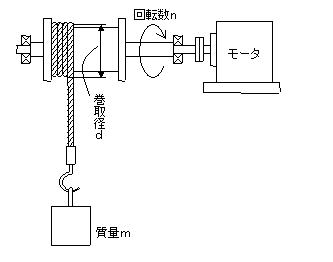
図のような巻き揚げ機において、質量m=2,000kgの重量物を巻取径d=400mm、巻取回転数n=120rpmで巻き揚げる場合について次の各問いに答えなさい。但し、重力加速度を9.81m/sec2とする。
(1)ロープの巻揚力はいくらか。
(2)モータの回転トルクはいくらか。
(3)必要なモーターパワー(所要動力)は何kW か。またそれは何馬力(PS)か。
|
| 〔解答〕 |
(1)質量m=2,000kgの物体に作用する重力Wは
W(N)=質量m(kg)×重力加速度9.81(m/sec2)
= 2,000(kg)× 9.81(m/sec2)
=19,620N
(2)巻取半径は、200mm(0.2m)であるから、巻取トルクTは、
T(Nm)=W(N)×R(m)=19,620N×0.2m=3,924Nm
(3)従って、必要なモーターパワー(動力)P(kW)は
P=Tn/9549=3,924Nm×120rpm/9549=49.3kW
また、 1kW=1.36馬力(PS)であるから、
P=49.3kW×1.36=67馬力
Ans (1) 19,620N、(2) 3,924Nm、(3)49.3kW、67馬力
|
|