| 情報 Information | ・エントロピーの話し(参考図1〜参考図6) |
| 参考図インデックス (タイトルをクリックして下さい。該当する図にジャンプします。) | |||
参考図1 〔容器Aと容器Bに水が入っています〕 参考図2 〔容器Aの水を温める〕 参考図3 〔容器Aのお湯を容器Bの水に混ぜる〕 参考図4 〔エントロピーの定義〕 参考図5(a) 〔容器Aのエントロピーの変化〕 参考図5(b) 〔容器Bのエントロピーの変化〕及び〔全体のエントロピーの変化〕 参考図6 〔熱量から仕事を取り出す実験〕 参考図7 〔容器Bから容器Aと同じ量の仕事を取り出す実験〕 |
|||
| 〔容器Aと容器Bに水が入っています〕 | |||
 |
|||
| 25℃の水50gが入った容器Aと25℃の水450gが入った容器Bがあります。大気の温度も25℃で、容器A、容器Bの水、大気の温度は皆同じで、平衡な状態にあります。 |
|||
| 参考図1 | |||
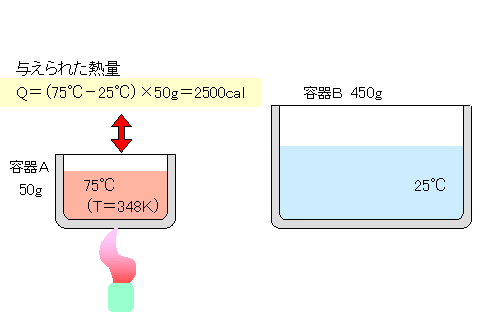
| 〔容器Aの水を温める〕 | |||
 |
|||
| 容器Aの25℃水50gを75℃まで温めます。容器Aの水には、2500cal の熱量が与えられたことになります。 |
|||
| 参考図2 | |||
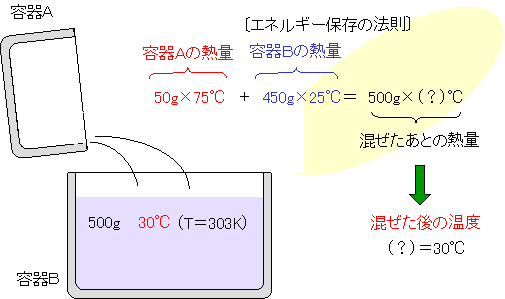
| 〔容器Aのお湯を容器Bの水に混ぜる〕 | |||
 |
|||
| 容器Aの75℃のお湯50g全部を、容器Bの25℃の水450gに混ぜます。混ぜる前と後のエネルギー(熱量)の総和は一定で、変わることがないという『エネルギー保存の法則』にしたがって計算すると、混ぜた後の水500gの温度は、30℃となります。 |
|||
| 参考図3 | |||
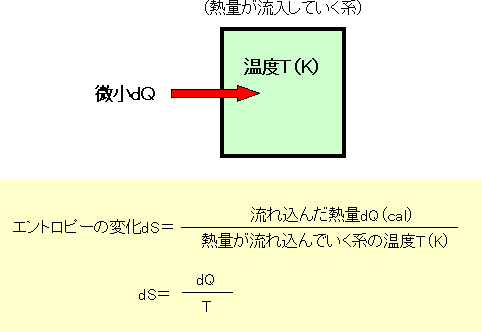
| 〔エントロピーの定義〕 | |||
 |
|||
| 温度がTの系に、微小の熱量dQが流れ込んだときの、エントロピーの変化dSは、〔流れ込んだ熱量(cal)〕を〔熱量が流れ込んでいく系の温度(K)〕で割った値です。 (※注) ここで、dQ、dSは、記号と考えて下さい。それぞれ、デルタキュー、デルタエスと読みます。 |
|||
| 参考図4 | |||
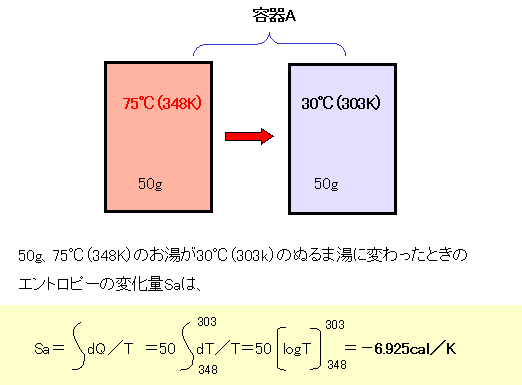
| 〔容器Aのエントロピーの変化〕 | |||
 |
|||
| 容器Aのお湯を容器Bの水に混ぜている過程で、容器Aのお湯の温度は刻々変わっていくので、積分を使って計算します。その計算結果(-6.925cal/K)だけに注目して頂ければ結構です。 |
|||
| 参考図5(a) | |||
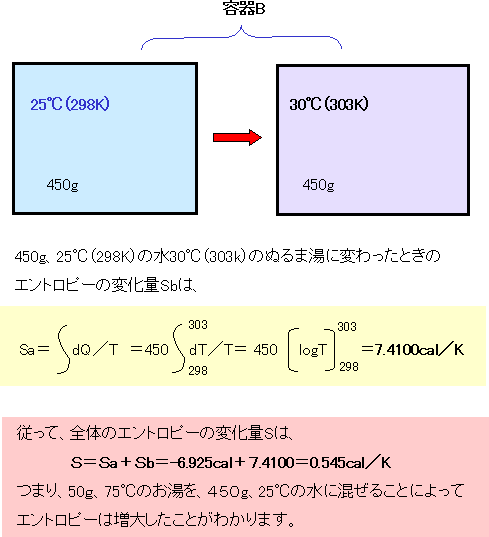
| 〔容器Bのエントロピーの変化〕及び〔全体のエントロピーの変化〕 | |||
 |
|||
| 容器Aのお湯を容器Bの水に混ぜている過程で、容器Bのお湯の温度は刻々変わっていくので、積分を使って計算します。その計算結果(7.4100cal/K)だけに注目して頂ければ結構です。容器Aのエンタルピーの変化と容器Bのエンタルピーの変化を加えると0.545cal/Kとります。つまり、お湯と水を混ぜる前より混ぜた後の方がエントロピーは増大しています。 |
|||
| 参考図5(b) | |||
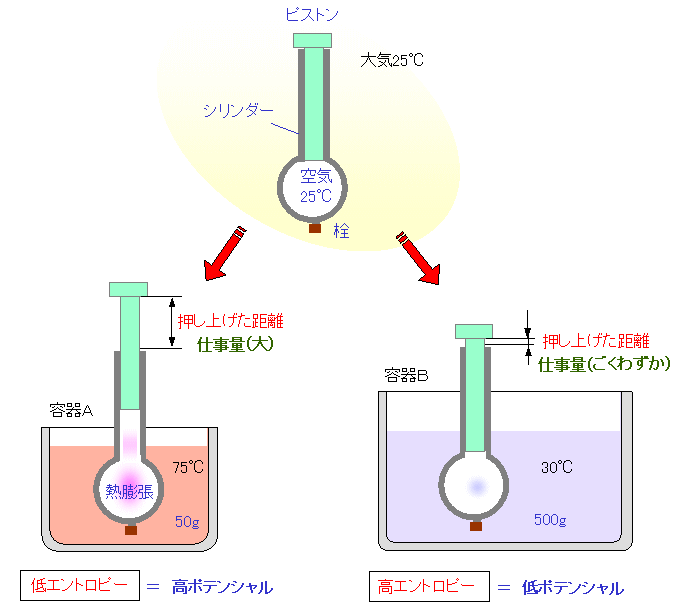
| 〔熱量から仕事を取り出す実験〕 | |||
 |
|||
| 注射器の球状部を容器Aの75℃のお湯の中に浸すと、球状内部の空気は暖められて熱膨張し、ピストンを押し上げます。すなわち、仕事を取り出すことができます。容器Bの30℃のぬるま湯の中に浸した場合は、球状内部の空気の熱膨張がごくわずかなため、ほとんど仕事を取り出すことができません。 |
|||
| 参考図6 | |||
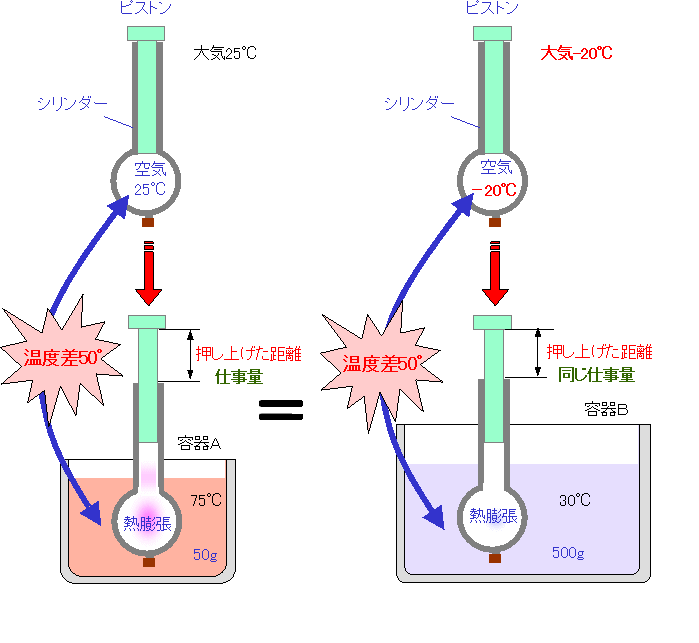
| 〔容器Bから容器Aと同じ量の仕事を取り出す実験〕 | |||
 |
|||
| 気温が−20℃の空気を注射器で吸入して実験をすれば、容器Bの30℃のぬるま湯からも容器Aの場合と同じ量の仕事を取り出すことができます。ポテンシャルを生み出しているのは、2つの熱源の温度差であることがわかります。 |
|||
| 参考図7 | |||